Мы начнем с рассмотрения основных уравнений для невязких жидкостей, выведенных Эйлером и Лагранжем. Пусть u = = u(x, t) означает вектор скорости жидкости в точке х в момент времени t. Пусть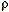 
(х, t) означает плотность жидкости, g(x, t)— внешнее гравитационное поле и р(х, t) — давление в жидкости.
Если принять правдоподобную гипотезу (Е) из 1 (игнорируя
молекулярную структуру вещества!), то легко показать, что
закон сохранения массы эквивалентен следующему уравнению в
частных производных:
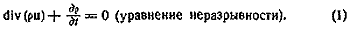
Если обозначить «субстанциональную» производную по времени для наблюдателя,
движущегося вместе с жидкостью, то можно переписать (1) в
виде
Случаю несжимаемости соответствует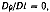 
и, следовательно, div u = 0.
При u = 0, когда жидкость находится в состоянии покоя, напряжение в жидкости на любой элемент поверхности действует по нормали к нему. Это — физическое определение жидкости; экспериментально проверено, что ему удовлетворяют многие реальные вещества.
Эйлер предположил, что этот закон гидростатики применим также к движущимся жидкостям, т. е. в гидродинамике. Этот закон приближенно удовлетворяется во многих случаях движения жидкостей (исключая области вблизи границы). Например, изменение скорости на 50 м/сек в слое воздуха толщиной в четверть миллиметра вызывает усилие сдвига, составляющее примерно 1/2000 атмосферного давления.
Непрерывные жидкости, удовлетворяющие гипотезе Эйлера, называются
невязкими., Как показал Коши, напряжение в невязкой жидкости
должно быть одинаковым во всех направлениях (изотропным);
получающаяся скалярная функция р(х, t) может быть названа
давлением. Далее, закон сохранения количества движения эквивалентен
следующему векторному уравнению в частных производных:
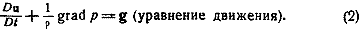
Для того чтобы получить замкнутую систему уравнений в частных производных, в которой все производные по времени могут быть выражены через производные по пространственным координатам к уравнениям (1), (2) нужно добавить еще одно соотношение. В теоретической механике однородных невязких жидкостей обычно вводится соотношение, связывающее плотность и давление.
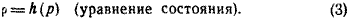
(3)
Баротропные течения. Невязкие жидкости, удовлетворяющие условию (3), могут быть названы баротропными, а движения жидкости, удовлетворяющие уравнениям (1) — (3),— «баротропными течениями», Эти течения встречаются в (приближенно) однородных жидкостях при условиях, которые являются термодинамически обратимыми. (Под «однородной жидкостью» мы понимаем жидкость, имеющую однородное строение, например чистую воду или воздух.)
Именно такие жидкости обычно рассматриваются в акустике и в аэродинамике больших скоростей. Быстрое сжатие и расширение — типичные адиабатические процессы в том смысле, что можно пренебречь теплопроводностью, Кроме того, пренебрежение теплопроводностью логически не противоречит пренебрежению вязкостью в уравнении (2), поскольку как теплопроводность, так и вязкость представляют собой молекулярные явления.
В случае идеального газа с термодинамическим уравнением
состояния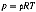 
и постоянным отношением теплоемкостей 
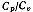элементарные рассуждения дают для адиабатического течения
соотношение
— так называемое политропное уравнение состояния для идеального термодинамически совершенного газа. Предельный случай т = 1 соответствует изотермическому течению (бесконечная теплоемкость или в бесконечном изотермическом резервуаре бесконечная проводимость).
Уравнение (За) достаточно точно для многих задач газовой динамики; для воздуха т = 1,4, Однако для жидкостей уравнение (3) необходимо брать другое уравнение.
Соотношение вида (3) является также приемлемым для жидкостей, которые только незначительно сжимаемы (т. е. при скоростях гораздо меньших скорости звука, особенно в обычных жидкостях). В этом случае можно просто писать
и говорить об однородной несжимаемой невязкой жидкость. Однако в этом случае уже нельзя выразить все производные по времени через производные по пространственным координатам.
