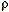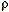U=U(x), =(х), g=g(х)

и т, д. — для осей координат, жестко связанных с телом, относительно которых жидкость движется с постоянной скоростью а. Ясно, что такие правдоподобные выводы основаны на гипотезе (В).

Если исходить из этих правдоподобных заключений, то далее можно действовать следующим образом, Для стационарных течений при U = U(x) уравнение движения (2) после однократного интегрирования по пространственным координатам становится эквивалентным уравнению:

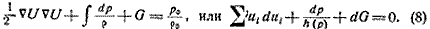
Это уравнение называется уравнением Бернулли для стационарного течения; в случае несжимаемой жидкости оно принимает известный простой вид:

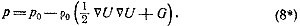
Подобным образом условие того, что скорость тела относительно жидкости на бесконечности равна может быть записано в виде:

и для несжимаемого, и для сжимаемого течения.

Наконец, поскольку течение стационарно, то должны быть стационарны и границы течения, Отсюда условие непроницаемости (7) сводится к условию

В случае безвихревого сжимаемого течения уравнение неразрывности (1) все еще можно записать при помощи единственной неизвестной функции U(x), Если только пренебречь эффектом гравитации, что обычно допустимо при достаточно больших скоростях, когда становится заметной сжимаемость'). (Если гравитацией нельзя пренебречь, как, например, в случае атмосферных движений больших масштабов, то условие (9) не может быть выполнено, даже несмотря на то, что безвихревое течение является допустимым)

Кинематика баротропного течения. Полагая G = О в уравнении (8), при описанных выше условиях мы можем получить равенство

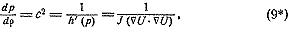
где х — функция, обратная функции 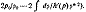. С другой стороны, из уравнения (1) при 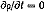следует 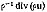, или:

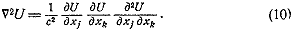
Другая форма уравнения (10) имеет вид:

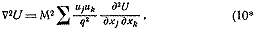
где локальное «число Маха» М = q/с есть отношение локальной скорости течения q к локальной скорости звука с, а все коэффициенты и;иь/ф меньше или равны 1.

Подставив в уравнение (10) выражение для 1/с', взятое из формулы (9а), мы получим уравнение

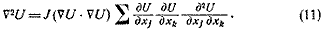
Одно-единственное уравнение в частных производных (11) вместе с краевыми условиями (9) и (7а) сводит задачу для случая стационарного занимаемого течения баротропной жидкости нулевой (малой?) вязкости к другой правдоподобной краевой задаче. Если только последняя задача решена, то из уравнения (8) можно легко найти поле давления.

Таким образом, мы свели задачу стационарного течения к чисто кинематической задаче. Если дано любое математическое решение уравнений (11), (9) и (7*) и если посредством уравнения (8) определено поле давления при G = О, то уравнение движения (2) удовлетворяется автоматически. Очевидно, что задача Неймана из параграфа 4 получается как предельный случай при с стремящемся к бесконечности. Допущение (F), таким образом, позволяет получить гораздо больше, а именно, что решение можно разложить по степеням М*2.