Более известным и более давним, чем парадокс
обратимости, является парадокс Даламбера, Согласно этому парадоксу,
из допущений, сделанных в параграфе 5, следует D = L = О.
Для случаев
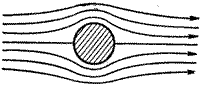
Р и с. 1. Обтекание цилиндра,
по Эйлеру.
кругового цилиндра (рис. 1) и сферы это следует, в силу
симметрии, из явной формы потенциала скоростей:

и теоремы Бернулли (8*) при g = О. Если задача корректно
поставлена, то наличие четырехкратной симметрии, как в данных
случаях, позволяет показать, что D = L = O, исходя только
из соображений обратимости.
Вообще же парадокс Даламбера следует из принципа обратимости
для любого профиля, который обладает центральной симметрией,
т. е для такого, который отображается в себя при отражении
относительно неподвижного центра симметрии. Обтекание плоской
пластинки на рис. 2, а дает пример подобного рода. Давления,
действующие на элементы поверхности, соответствующие друг
другу при центральной симметрии, равны по величине и противоположны
по направлению. Следовательно, эта система сил сводится
только к паре сил.
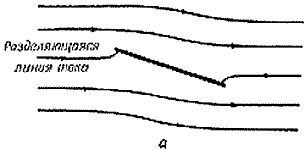
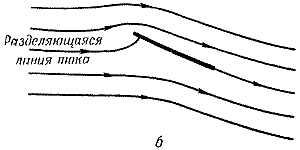

Р и с. 2. Обтекание плоской пластинки,
по Эйлеру (а), по Жуковскому (б) и по Гельмгольцу (в).
Демонстрация парадокса а общем случае дело довольно тон.
кое, при этом используется сложная теорема о поведении решений
уравнения V'U = O нa бесконечности. А именно, пусть U(x)
возрастает на бесконечности, по крайней мере, как первая
степень модуь x = r. Тогда можно показать, что
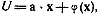
где 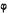 (x)
«регулярна на бесконечности». Под этим мы понимаем то, что
(x)
«регулярна на бесконечности». Под этим мы понимаем то, что
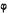 (x) можно
разложить в некоторый сходящийся ряд (аналогичный ряду по
отрицательным степеням в разложении Лорана), члены которого
суть произведения отрицательных степеней r и сферических
гармоник, выраженных через широту и долготу.
(x) можно
разложить в некоторый сходящийся ряд (аналогичный ряду по
отрицательным степеням в разложении Лорана), члены которого
суть произведения отрицательных степеней r и сферических
гармоник, выраженных через широту и долготу.